回溯算法
回溯算法是一个枚举过程,在搜索中寻找问题解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。
框架
res = []
def backtrack(当前路径,选择列表):
if 满足条件:
res.append(path)
return
for 值 in 选择列表:
加入到当前路径
backtrack(当前路径,选择条件)
从当前路径弹出
经典题目
全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1]
输出:[[1]]
提示:
1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同
图形展示
这张图取自网络
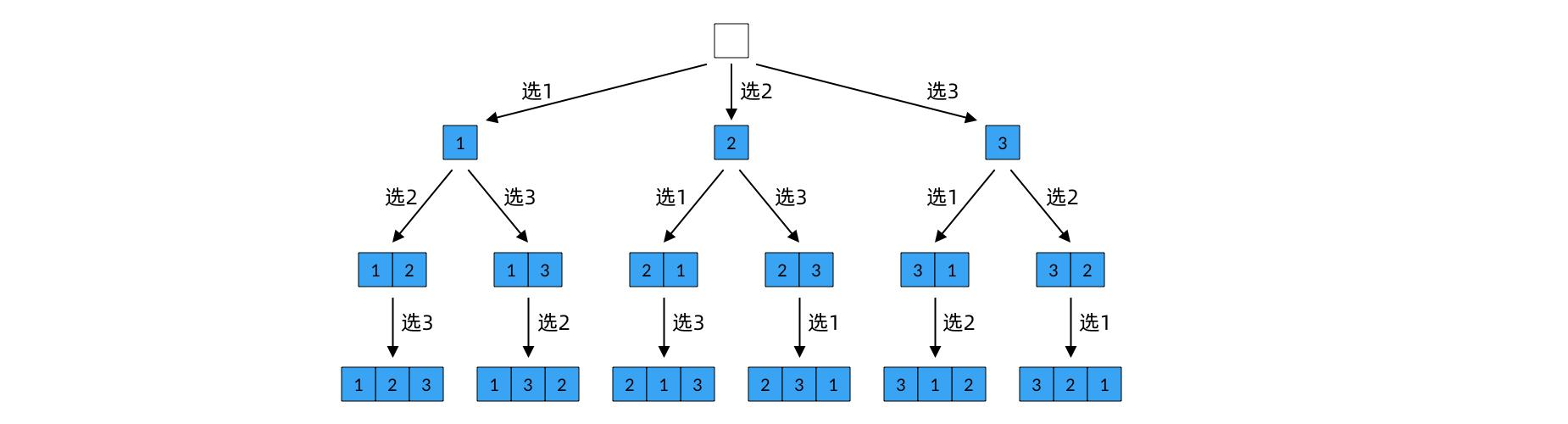
解答
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
def backtrack(nums, n, used, path, ret):
if len(path) == n:
ret.append(path[:])
return
for i in range(n):
if used[i]:
continue
used[i] = True
path.append(nums[i])
backtrack(nums, n, used, path, ret)
used[i] = False
path.pop()
ret = []
n = len(nums)
backtrack(nums, n,[False] *n, [], ret)
return ret
子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
提示:
1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同
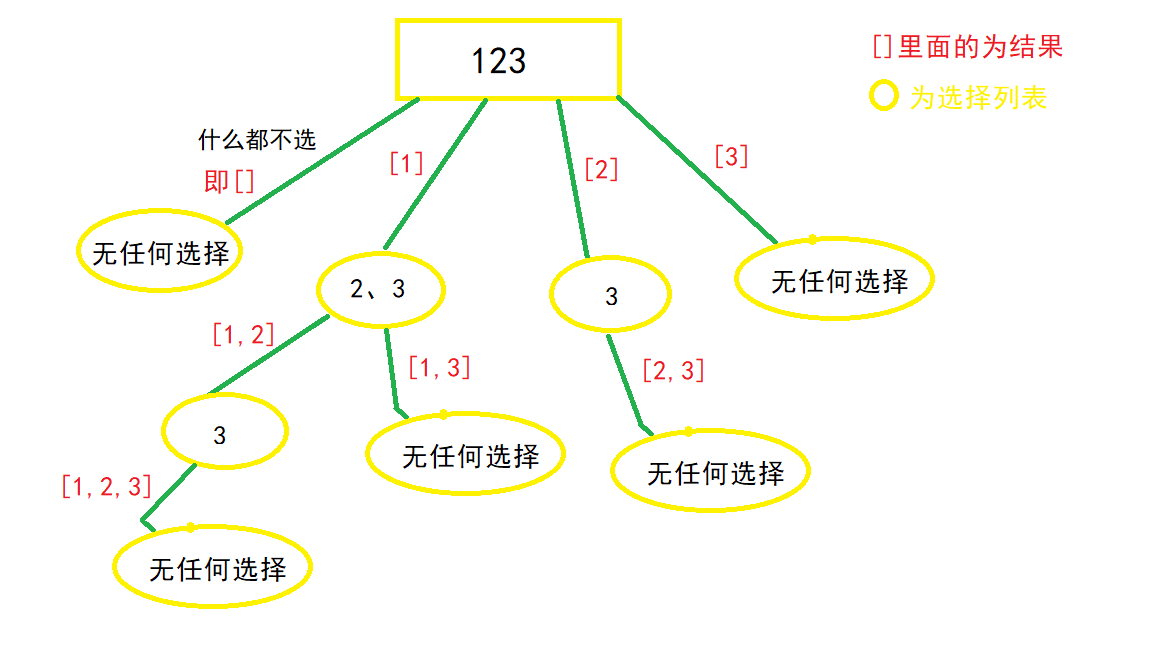
图解
本图来自于leetcode题解中,地址:https://leetcode-cn.com/problems/subsets/solution/c-zong-jie-liao-hui-su-wen-ti-lei-xing-dai-ni-gao-/
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
def backtrack(nums, n, index, path, ret):
if index == n:
# 结束条件
return
# 以index为起始值
for i in range(index, n):
path.append(nums[i])
# 存储路径结果,path[:]拷贝值
ret.append(path[:])
backtrack(nums, n, i + 1, path, ret)
path.pop()
# 默认添加[]
ret = [[]]
n = len(nums)
backtrack(nums, n, 0, [], ret)
return ret
八皇后
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
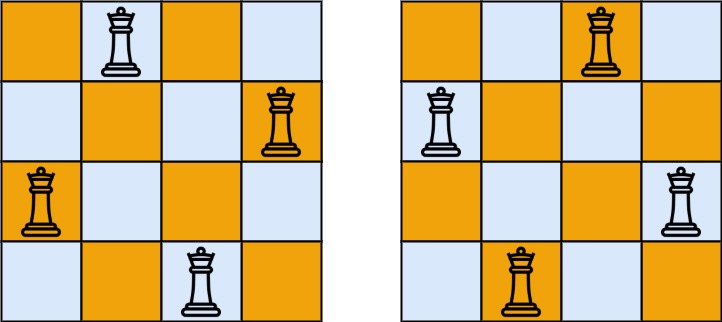
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:[["Q"]]
提示:
1 <= n <= 9
皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
N皇后
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
def check_valid(board, row, col):
'''检查当前位置是否合理, 检查3个方向就行,上方,左上和右上'''
# 检查上方
for i in range(row - 1, -1, -1):
if board[i][col] == 'Q':
return False
# 检查左上
i = row - 1
j = col - 1
while i >= 0 and j >= 0:
if board[i][j] == 'Q':
return False
i -= 1
j -= 1
# 检查右下方
i = row - 1
j = col + 1
while i >= 0 and j < n:
if board[i][j] == 'Q':
return False
i -= 1
j += 1
return True
def backtrack(n, row, board, ret):
if row == n:
# 已经到达最底层,加入到结果集中
ret.append([''.join(row) for row in board])
return
for col in range(n):
if not check_valid(board, row, col):
continue
board[row][col] = 'Q'
backtrack(n, row + 1, board, ret)
board[row][col] = '.'
board = [['.' for _ in range(n)] for _ in range(n)]
ret = []
backtrack(n, 0, board, ret)
return ret