递归
在数学与计算机科学中,递归(Recursion)是指在函数的定义中使用函数自身的方法。实际上,递归,顾名思义,其包含了两个意思:递 和 归,这正是递归思想的精华所在。
递归伪代码
def recursion(参数):
if 结束条件:
return
处理问题
recursion(缩小参数)
汉诺塔问题
在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。
请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
示例1:
输入:A = [2, 1, 0], B = [], C = []
输出:C = [2, 1, 0]
示例2:
输入:A = [1, 0], B = [], C = []
输出:C = [1, 0]
提示:
A中盘子的数目不大于14个。
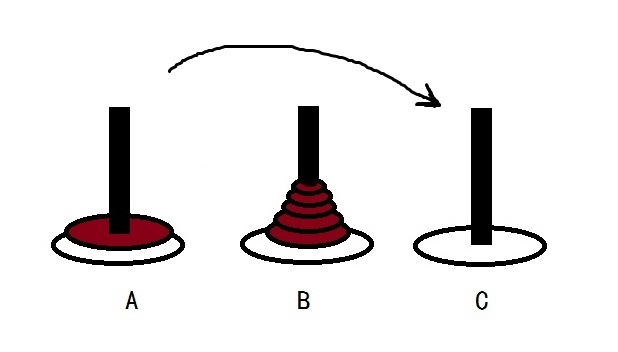
n = 1 时,直接把盘子从 A 移到 C; n > 1 时, 1. 先把上面 n - 1 个盘子从 A 移到 B; 2. 再将最大的盘子从 A 移到 C; 3. 再将 B 上 n - 1 个盘子从 B 移到 C
class Solution:
def hanota(self, A: List[int], B: List[int], C: List[int]) -> None:
"""
Do not return anything, modify C in-place instead.
"""
def move(n, A, B, C):
if n == 1:
C.append(A[-1])
A.pop()
return
# 将n-1个盘子从A借助C移动到B上
move(n - 1, A, C, B)
# 将A中最后一个盘子放到C中
C.append(A[-1])
A.pop()
# 将n-1个盘子从B借助A放到C上
move(n - 1, B, A, C)
n = len(A)
move(n, A, B, C)
24. 两两·交换链表中的节点
给定一个链表,两两交换其中相邻的节点,并返回交换后的链表。
你不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
示例 1:
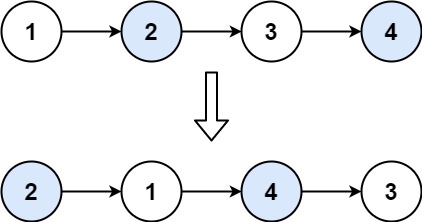
输入:head = [1,2,3,4]
输出:[2,1,4,3]
示例 2:
输入:head = []
输出:[]
示例 3:
输入:head = [1]
输出:[1]
提示:
链表中节点的数目在范围 [0, 100] 内
0 <= Node.val <= 100
解题思路
链表很多的问题都会用到递归算法,这个也不例外,既然题目要求我们,我们可以把问题进行拆分,先将前两个节点进行交换,然后递归的将剩余的节点进行反转
答案
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
# Definition for singly-linked list.
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
class Solution:
def swapPairs(self, head: ListNode) -> ListNode:
# 判断是否有两个合法的节点
if head is None or head.next is None:
return head
# 头结点
cur = head
# 下一个节点
nextNode = head.next
# 剩余节点
otherNode = nextNode.next
# 进行节点交换
nextNode.next = cur
# 反转剩余节点
cur.next = self.swapPairs(otherNode)
return nextNode
669. 修剪二叉搜索树
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树不应该改变保留在树中的元素的相对结构(即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在唯一的答案。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
提示:
树中节点数在范围 [1, 104] 内
0 <= Node.val <= 104
树中每个节点的值都是唯一的
题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 104
示例1
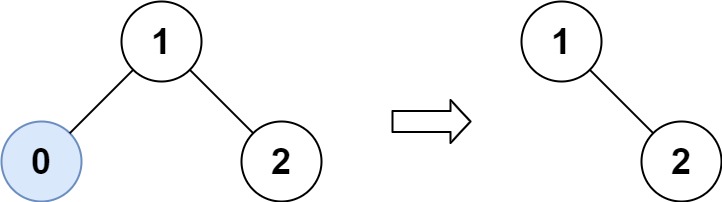
输入:root = [1,0,2], low = 1, high = 2
输出:[1,null,2]
示例2
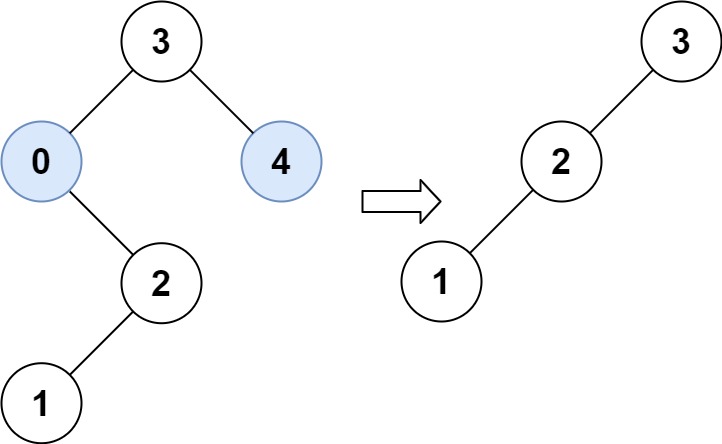
输入:root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出:[3,2,null,1]
示例 3:
输入:root = [1], low = 1, high = 2
输出:[1]
示例 4:`
输入:root = [1,null,2], low = 1, high = 3
输出:[1,null,2]
示例 5:
输入:root = [1,null,2], low = 2, high = 4
输出:[2]
答案
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def trimBST(self, root: TreeNode, low: int, high: int) -> TreeNode:
if root is None:
return root
if root.val < low:
# 如果当前节点小于low,那根据二叉搜索树特性,那么root的left节点肯定都小于low,不符合条件,要舍弃root和root.left,直接将root的right节点变成root
root = root.right
# 进行后面的节点判断
return self.trimBST(root, low, high)
elif root.val > high:
# 反之同理,将root和root.right舍弃
root = root.left
return self.trimBST(root, low, high)
# 当前root.val在区间[low, high]中,分别对left和right节点进行判断
root.left = self.trimBST(root.left, low, high)
root.right = self.trimBST(root.right, low, high)
return root
链表反转
输入:1->2->3->4->5
输出: 5->4->3->2->1
# class Node:
# def __init__(self, val):
# self.val = val
# self.next = None
class Solution:
def reverse(self, root: Node) -> Node:
def recursion(prev: Node, cur: Node):
if not cur:
# 返回prev节点
return prev
nextNode = cur.next
cur.next = prev
prev = cur
return recursion(prev, nextNode)
prev = None
cur = root
return recursion(prev, cur)